Lecture 3 - Neural network deep dive#

A deep dive into optimising neural networks with stochastic gradient descent

Learning objectives#

Understand how to implement neural networks from scratch
Understand all the ingredients needed to define a Learner in fastai

References#

Chapter 4 of Deep Learning for Coders with fastai & PyTorch by Jeremy Howard and Sylvain Gugger.
What is torch.nn really? by Jeremy Howard.

Setup#

# Uncomment and run this cell if using Colab, Kaggle etc
# %pip install fastai==2.6.0 datasets

Imports#

import math

import torch
from datasets import load_dataset
from fastai.tabular.all import *
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from torch.utils.data import DataLoader, TensorDataset
from tqdm.auto import tqdm

import datasets

# Suppress logs to keep things tidy
datasets.logging.set_verbosity_error()

The dataset#

In lecture 2, we focused on optimising simple functions with stochastic gradient descent. Let’s now tackle a real-world problem using neural networks! We’ll use the \(N\)-subjettiness dataset from lecture 1 that represents jets in terms of \(\tau_N^{(\beta)}\) variables that measure the radiation about \(N\) axes in the jet according to an angular exponent \(\beta>0\). As usual, we’ll load the dataset from the Hugging Face Hub and convert it to a Pandas DataFrame via the to_pandas() method:

nsubjet_ds = load_dataset("dl4phys/top_tagging_nsubjettiness")
df = nsubjet_ds["train"].to_pandas()
df.head()

	pT	mass	tau_1_0.5	tau_1_1	tau_1_2	tau_2_0.5	tau_2_1	tau_2_2	tau_3_0.5	tau_3_1	...	tau_4_0.5	tau_4_1	tau_4_2	tau_5_0.5	tau_5_1	tau_5_2	tau_6_0.5	tau_6_1	tau_6_2
0	543.633944	25.846792	0.165122	0.032661	0.002262	0.048830	0.003711	0.000044	0.030994	0.001630	...	0.024336	0.001115	0.000008	0.004252	0.000234	7.706005e-07	0.000000	0.000000	0.000000e+00
1	452.411860	13.388679	0.162938	0.027598	0.000876	0.095902	0.015461	0.000506	0.079750	0.009733	...	0.056854	0.005454	0.000072	0.044211	0.004430	6.175314e-05	0.037458	0.003396	3.670517e-05
2	429.495258	32.021091	0.244436	0.065901	0.005557	0.155202	0.038807	0.002762	0.123285	0.025339	...	0.078205	0.012678	0.000567	0.052374	0.005935	9.395772e-05	0.037572	0.002932	2.237277e-05
3	512.675443	6.684734	0.102580	0.011369	0.000170	0.086306	0.007760	0.000071	0.068169	0.005386	...	0.044705	0.002376	0.000008	0.027895	0.001364	4.400042e-06	0.009012	0.000379	6.731099e-07
4	527.956859	133.985415	0.407009	0.191839	0.065169	0.291460	0.105479	0.029753	0.209341	0.049187	...	0.143768	0.033249	0.003689	0.135407	0.029054	2.593460e-03	0.110805	0.023179	2.202088e-03

5 rows × 21 columns

Preparing the data#

In lecture 1, we used the TabularDataLoaders.from_df() method from fastai to quickly create dataloaders for the train and validation sets. In this lecture, we’ll be working with PyTorch tensors directly, so we’ll take a different approach. To get started, we’ll need to split our data into training and validation sets. We can do this easily via the train_test_split() function from scikit-learn:

train_df, valid_df = train_test_split(df, random_state=42)
train_df.shape, valid_df.shape

((908250, 21), (302750, 21))

This has allocated 75% of our original dataset to train_df and the remainder to valid_df. Now that we have these DataFrames, the next thing we’ll need are tensors for the features \((p_T, m, \tau_1^{(0.5)}, \tau_1^{(1)}, \tau_1^{(2)}, \ldots )\) and labels. There is, however, one potential problem: the jet \(p_T\) and mass have much larger scales than the \(N\)-subjettiness \(\tau_N^{(\beta)}\) features. We can see this by summarising the statistics of the training set with the describe() function:

train_df.describe()

	pT	mass	tau_1_0.5	tau_1_1	tau_1_2	tau_2_0.5	tau_2_1	tau_2_2	tau_3_0.5	tau_3_1	...	tau_4_0.5	tau_4_1	tau_4_2	tau_5_0.5	tau_5_1	tau_5_2	tau_6_0.5	tau_6_1	tau_6_2	label
count	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	...	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000	908250.000000
mean	487.107393	88.090520	0.366716	0.198446	0.319559	0.222759	0.079243	0.072535	0.148137	0.035372	...	0.112024	0.022150	0.008670	0.088400	0.015329	0.004875	0.070679	0.011019	0.002914	0.500366
std	48.568267	48.393646	0.186922	0.339542	2.003898	0.110955	0.125155	0.674091	0.072627	0.051869	...	0.059393	0.032004	0.155468	0.051949	0.022866	0.107641	0.046571	0.017133	0.078247	0.500000
min	225.490387	-0.433573	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
25%	452.879289	39.958178	0.224456	0.058381	0.006443	0.139269	0.025638	0.001565	0.094603	0.013308	...	0.069037	0.007949	0.000188	0.051012	0.004936	0.000079	0.036142	0.002977	0.000033	0.000000
50%	485.894050	99.887418	0.380172	0.166016	0.045887	0.222763	0.061597	0.008788	0.148810	0.028501	...	0.110220	0.017609	0.000787	0.086045	0.011755	0.000387	0.067797	0.008028	0.000193	1.000000
75%	520.506446	126.518545	0.477122	0.240550	0.074417	0.299708	0.108207	0.022441	0.196156	0.046588	...	0.151137	0.029990	0.002006	0.121905	0.021089	0.001103	0.100437	0.015359	0.000635	1.000000
max	647.493145	299.211555	2.431888	6.013309	37.702422	2.218956	5.392683	33.352249	1.917912	4.502011	...	1.616280	3.753716	21.161948	1.407356	3.158352	17.645603	1.388879	3.127371	17.340970	1.000000

8 rows × 21 columns

Here we can see that the jet \(p_T\) and mass have average values of around 480 and 90 GeV, while the \(N\)-subjettiness variables \(\tau_N^{(\beta)}\) have values that are orders of magnitude smaller. As we saw in lecture 2, SGD can struggle to optimise the loss function when the feature scales are very different. To handle this, it is common to normalize the features. One way to do this is by rescaling all the features \(x_i\) to lie in the interval \([0,1]\):

\[ x_i' = \frac{x_i - x_{i,\mathrm{min}}}{x_{i,\mathrm{max}} - x_{i,\mathrm{min}}} \]

To apply this minmax normalization, let’s first grab the NumPy arrays of the features and labels:

# Slice out all feature columns
train_x = train_df.iloc[:, :-1].values
# Slice out the label column
train_y = train_df.iloc[:, -1].values

Next, we use the MinMaxScaler from scikit-learn to apply the normalization on the features array:

scaler = MinMaxScaler()
train_x = scaler.fit_transform(train_x)
# Sanity check the normalization worked
np.min(train_x), np.max(train_x)

(0.0, 1.0)

Great, this worked! Now that our features are all nicely normalised, let’s convert these NumPy arrays to PyTorch tensors. PyTorch provides a handy from_numpy() method that allows us to do the conversion easily:

# Cast to float32
train_x = torch.from_numpy(train_x).float()
train_y = torch.from_numpy(train_df.iloc[:, -1].values)
# Sanity check on the shapes
train_x.shape, train_y.shape

(torch.Size([908250, 20]), torch.Size([908250]))

Okay, now that we have our tensors it’s time to train a neural network!

Logistic regression as a neural network#

To warm up, let’s train the simplest type of neural network for classification tasks: logistic regression! You might be surprised to hear that logistic regression can be viewed as a neural network. However, a one-layer network has the same properties, so let’s look at how we can implement this in PyTorch.

To get started, we’ll need some weights and biases, so let’s create random tensors using a type of intialization called Xavier initialization. This initializes the biases to zero, while the weights \(W_{ij}\) are sampled from a normal distribution in the interval \((-1/\sqrt{n},1/\sqrt{n})\), where \(n\) is the number of features. We can implement Xavier initialization in PyTorch as follows:

set_seed(42)
# Xavier initialisation
weights = torch.randn(20, 2) / math.sqrt(20)
# Track grads after initialization
weights.requires_grad_()
bias = torch.zeros(2, requires_grad=True)

Now that we have the weights and biases, the next ingredient we need is an activation function. For binary classification tasks, this usually takes the form of a sigmoid function, whose generalization to \(K>2\) classes is called the softmax function:

\[ \sigma(\mathbf{x})_i = \frac{e^{x_i}}{\sum_{j=1}^K e^{x_j}} \qquad \mbox{for } i=1, \ldots , K\]

The sigmoid and the softmax functions have the effect of normalizing the output of the network to be a probability distribution. To keep things general, we’ll use the softmax in this lecture. However, implementing softmax naively presents some numerical stability challenges. Consider, for example, computing the following:

x = torch.tensor([1000.0, 1000.0, 1000.0])
x.exp()

tensor([inf, inf, inf])

Hmm, a network that outputs infinity values will will cause the learning process to crash. This is an example of numerical overflow. Similarly, when the inputs are large negative numbers, we end up rounding the results to zero, an example of numerical underflow:

x = torch.tensor([-1000.0, -1000.0, -1000.0])
x.exp()

tensor([0., 0., 0.])

To deal with these two problems, we can apply the log-sum-exp trick:

\[\log \sum_{i=1}^n e^{x_i} = a + \log \sum_{i=1}^n e^{x_i-a} \]

where \(a = \max x_i\) is a constant that forces the greatest value to be zero. Since \(\log a/b = \log a - \log b\), taking the logarithm of the softmax function gives:

def log_softmax(x):
    return (x - x.max()) - (x - x.max()).exp().sum(-1).log().unsqueeze(-1)


log_softmax(x)

tensor([-1.0986, -1.0986, -1.0986])

Great, we now have an activation function that is numerically stable. Let’s now define our logistic regression model to take a mini-batch xb of inputs and output the log-softmax values:

def model(xb):
    return log_softmax(xb @ weights + bias)

Let’s test this model with a batch of data from our training set (also called a forward pass):

# Batch size
bs = 1024
# A mini-batch from x
xb = train_x[0:bs]
# Model predictions
preds = model(xb)
preds[0], preds.shape

(tensor([-0.5103, -0.9171], grad_fn=<SelectBackward0>), torch.Size([1024, 2]))

At this state the predictions are random, since we started with random weights. To improve these values, the next thing we need is a loss function. For classification tasks, one computes the cross entropy, which is the log likelihood of the softmax:

\[ {\cal L} = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K y_k^{(i)}\log\hat{p}_k^{(i)} \,.\]

However, we’ve already taken the log of the softmax values \(\hat{p}_k^{(i)}\), so instead our loss will be the negative log likelihood, which doesn’t include the logarithm. We can implement this easily in PyTorch as follows:

def nll_loss(predictions, target):
    # Mask predictions according to whether y_hat is 1 or 0
    return -predictions[range(target.shape[0]), target].mean()


loss_func = nll_loss

Now that we have a loss function, let’s test we can compute the loss by comparing our mini-batch of predictions against a mini-batch of target values:

yb = train_y[0:bs]
print(loss_func(preds, yb))

tensor(0.7619, grad_fn=<NegBackward0>)

Again, the loss value is random, but we can minimise this function with backpropagation. Before doing that, let’s also compute the accuracy of the model so that we track progress during training:

def accuracy(out, yb):
    preds = torch.argmax(out, dim=1)
    return (preds == yb).float().mean()


accuracy(preds, yb)

tensor(0.5020)

Indeed, the random model has an accuracy of 50% which is what we expect before any training. To implement the training loop, we’ll take the following steps:

Select a mini-batch of data of size bs
Generate predictions from the model by computing the forward pass
Compute the loss
Compute the gradients of the loss wrt to the parameters by applying loss.backward()
Update the weights and biases of the model by taking a step of gradient descent

In code, this looks as follows:

# Learning rate
lr = 1e-2
# Number of epochs
epochs = 3
n = len(train_df)

for epoch in tqdm(range(epochs), desc="num_epochs"):
    for i in tqdm(range((n - 1) // bs + 1), leave=False):
        # 1. Select mini-batch
        start_i = i * bs
        end_i = start_i + bs
        xb = train_x[start_i:end_i]
        yb = train_y[start_i:end_i]
        # 2. Generate predictions
        pred = model(xb)
        # 3. Compute the loss
        loss = loss_func(pred, yb)
        # 4. Compute the gradients
        loss.backward()
        # 5. Update the weights and biases
        with torch.no_grad():
            weights -= weights.grad * lr
            bias -= bias.grad * lr
            # Set current gradients to zero
            weights.grad.zero_()
            bias.grad.zero_()

Note that here we update the weights and biases within the torch.no_grad() context manager - that’s because we don’t want these updates to be recorded in the tensors in the next iteration of gradient descent. We also set the gradients to zero after the update to prevent tracking these operations with every iteration.

Now that we’ve trained our model, let’s compute the loss and accuracy to see if they’ve improved:

def print_scores():
    print(f"Loss: {loss_func(model(xb), yb):.3f}")
    print(f"Accuracy: {accuracy(model(xb), yb):.3f}")

print_scores()

Loss: 0.561
Accuracy: 0.857

Congratulations - you’ve trained your first neural network from scratch!

In principle, there’s nothing wrong with using raw PyTorch tensor operations to train models, but the framework provides various functions and classes that can simplify our code and make it more robust to errors. Let’s take a look.

Refactoring with PyTorch’s functional API#

Instead of manually computing the log-softmax and negative log-likelihood, PyTorch provide a cross-entropy function that does all of this in one go! This function and many others live within the torch.nn.functional module, which is usually imported into the F namespace. Let’s use the F.cross_entropy function as our loss function, which means we can remove the activation from our model’s forward pass:

loss_func = F.cross_entropy

def model(xb):
    return xb @ weights + bias

# Sanity check we get the same scores as before
print_scores()

Loss: 0.561
Accuracy: 0.857

Refactoring with PyTorch’s `nn` classes#

The next thing we’ll do is simplify our training loop by using the nn.Module and nn.Parameter classes. The first holds the weights and biases of the model, and defines the forward pass. The second, makes it simpler to keep track of the gradients:

class LogisticRegressor(nn.Module):
    def __init__(self):
        super().__init__()
        self.weights = nn.Parameter(torch.randn(20, 2) / math.sqrt(20))
        self.bias = nn.Parameter(torch.zeros(2))

    def forward(self, xb):
        return xb @ self.weights + self.bias

Now when we instantiate this class, we get a newly initialized model, which we can generate predictions from, compute the loss etc:

model = LogisticRegressor()
loss_func(model(xb), yb)

tensor(0.7114, grad_fn=<NllLossBackward0>)

The big advatnage of the nn.Module and nn.Parameter classes is that we no longer have to manually update each parameter by name and zero out the gradients. We just need to iterate over the parameters associated with nn.Module and apply model.zero_grad() at the end of the updates. Let’s wrap the training loop in a fit() function for later use:

def fit():
    for epoch in tqdm(range(epochs), desc="num_epochs"):
        for i in tqdm(range((n - 1) // bs + 1), leave=False):
            # 1. Select mini-batch
            start_i = i * bs
            end_i = start_i + bs
            xb = train_x[start_i:end_i]
            yb = train_y[start_i:end_i]
            # 2. Generate predictions
            pred = model(xb)
            # 3. Compute the loss
            loss = loss_func(pred, yb)
            # 4. Compute the gradients
            loss.backward()
            # 5. Update the weights and biases
            with torch.no_grad():
                for p in model.parameters():
                    p -= p.grad * lr
                model.zero_grad()


fit()
print_scores()

Loss: 0.547
Accuracy: 0.859

We can actually simplify our model even further by using the nn.Linear class, which defines a linear layer in a neural network. This class automatically initializes the weights and biases with Xavier initialization and computes xb @ weights + biases for us. Let’s use this layer and retrain our model:

class LogisticRegressor(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(20, 2)

    def forward(self, xb):
        return self.linear(xb)


model = LogisticRegressor()
fit()
print_scores()

Loss: 0.530
Accuracy: 0.859

It works!

Refactoring with PyTorch optimizers#

Now let’s simplify the gradient update step of our training loop by using the SGD optimizer in PyTorch. This optimizer will allow us to reduce the whole logic under the torch.no_grad() context manager with just two steps:

# 5. Update the weights and biases
optimizer.step()
optimizer.zero_grad()

To do so, let’s create a simple helper function that initializes a new model and optimizer:

def get_model():
    model = LogisticRegressor()
    return model, torch.optim.SGD(model.parameters(), lr=lr)


model, optimizer = get_model()
loss_func(model(xb), yb)

tensor(0.7052, grad_fn=<NllLossBackward0>)

Now that we have a model and optimizer, we can refactor our fit() function as follows:

def fit():
    for epoch in tqdm(range(epochs), desc="num_epochs"):
        for i in tqdm(range((n - 1) // bs + 1), leave=False):
            # 1. Select mini-batch
            start_i = i * bs
            end_i = start_i + bs
            xb = train_x[start_i:end_i]
            yb = train_y[start_i:end_i]
            # 2. Generate predictions
            pred = model(xb)
            # 3. Compute the loss
            loss = loss_func(pred, yb)
            # 4. Compute the gradients
            loss.backward()
            # 5. Update the weights and biases
            optimizer.step()
            optimizer.zero_grad()


fit()
print_scores()

Loss: 0.535
Accuracy: 0.859

Nice, our training loop is quite concise now, but notice that we still have to manually define the mini-batches. Let’s see how we can simplify this with the Dataset and DataLoader classes in PyTorch.

Refactoring with `Dataset` classes#

PyTorch provides an abstract Dataset class that simplifies the way we access the features and labels of each mini-batch. The main requirement is that a Dataset should implement __len__ and __getitem__ functions that allow us to iterate over the data. PyTorch conveniently provides a TensorDataset that does this for tensors, so we can create our dataset by simply passing the tensors of features and labels:

train_ds = TensorDataset(train_x, train_y)

This dataset has a length:

len(train_ds)

and we can index into it like a Python list:

train_ds[0]

(tensor([6.1467e-01, 3.4553e-01, 2.0827e-01, 6.1930e-02, 2.9217e-02, 1.1426e-01,
         3.9722e-02, 3.0127e-02, 1.1553e-01, 4.4638e-02, 3.7694e-02, 1.1224e-01,
         5.0610e-02, 4.7183e-02, 7.6042e-02, 4.5295e-03, 2.0119e-05, 5.5926e-02,
         2.8786e-03, 8.6186e-06]),
 tensor(1))

Note that each element returns a tuple of the feature and corresponding label. This means we can replace the mini-batch step to a single line of code:

xb, yb = train_ds[i * bs : i * bs + bs]

Let’s refactor our fit() function to use the train_ds object now:

model, optimizer = get_model()


def fit():
    for epoch in tqdm(range(epochs), desc="num_epochs"):
        for i in tqdm(range((n - 1) // bs + 1), leave=False):
            # 1. Select mini-batch
            xb, yb = train_ds[i * bs : i * bs + bs]
            # 2. Generate predictions
            pred = model(xb)
            # 3. Compute the loss
            loss = loss_func(pred, yb)
            # 4. Compute the gradients
            loss.backward()
            # 5. Update the weights and biases
            optimizer.step()
            optimizer.zero_grad()


fit()
print_scores()

Loss: 0.545
Accuracy: 0.856

Refactoring with DataLoaders#

We can actually simplify our training loop even further by using a PyTorch DataLoader class to manage the way we grab mini-batches. A DataLoader receives a Dataset and returns a generator we can iterate over:

train_ds = TensorDataset(train_x, train_y)
train_dl = DataLoader(train_ds, batch_size=bs, shuffle=True)
next(iter(train_dl))

[tensor([[3.1934e-01, 3.0916e-01, 1.7249e-01,  ..., 5.0833e-02, 2.5030e-03,
          6.6223e-06],
         [5.9345e-01, 1.3606e-01, 1.0415e-01,  ..., 6.3039e-02, 3.7498e-03,
          2.1251e-05],
         [7.4757e-01, 3.8743e-01, 1.3758e-01,  ..., 2.7057e-02, 1.9911e-03,
          2.2671e-05],
         ...,
         [5.9834e-01, 3.3535e-01, 1.8187e-01,  ..., 2.6380e-02, 1.0312e-03,
          1.8795e-06],
         [6.3238e-01, 4.1819e-01, 1.7070e-01,  ..., 6.9010e-02, 5.0007e-03,
          1.0914e-04],
         [7.1288e-01, 9.3378e-02, 6.7393e-02,  ..., 2.5031e-02, 7.3758e-04,
          2.1064e-06]]),
 tensor([1, 0, 1,  ..., 1, 1, 0])]

We can then simply iterate over the DataLoader to get our mini-batches for the model:

model, optimizer = get_model()


def fit():
    for epoch in tqdm(range(epochs), desc="num_epochs"):
        # 1. Select mini-batch
        for xb, yb in tqdm(train_dl, leave=False):
            # 2. Generate predictions
            pred = model(xb)
            # 3. Compute the loss
            loss = loss_func(pred, yb)
            # 4. Compute the gradients
            loss.backward()
            # 5. Update the weights and biases
            optimizer.step()
            optimizer.zero_grad()


fit()
print_scores()

Loss: 0.537
Accuracy: 0.858

Great, we now have a rather simple training loop that works with any type of model! Let’s now use a full-blown neural network with several hidden layers!

Going deeper#

Our logistic regression model is actually pretty good, but in many applications you’ll want a deep neural network to get better performance. To create neural networks, PyTorch provides a nn.Sequential class that allows you to stack layers one after another. Let’s implement the same architecture defined in the top tagging review from the top tagging review:

The network consists of four fully connected hidden layers, the first two with 200 nodes and a dropout regularization of 0.2, and the last two with 50 nodes and a dropout regularization of 0.1. The output layer consists of two nodes. We use a ReLu activation function throughout and minimize the cross-entropy using Adam optimization

We briefly encountered dropout in the last lecture, so let’s quckly explain how it works. Dropout is a regularization technique (not the type of regularization you’re familiar from QFT though!), that is designed to prevent the model from overfitting. The basic idea is to randomly change some of the activations in the network to zero during training time. An animation of the process is shown below, which shows how this process introduces some noise into the process and produces a more robust network:

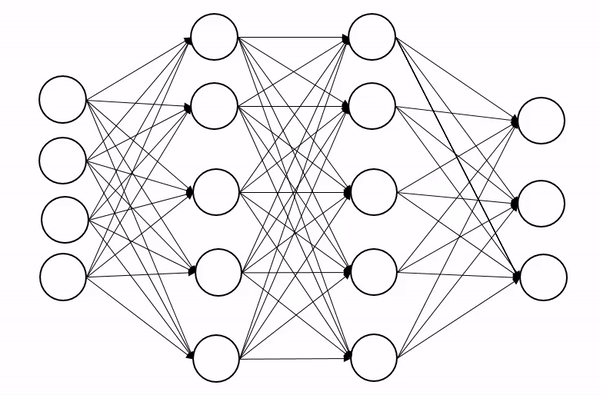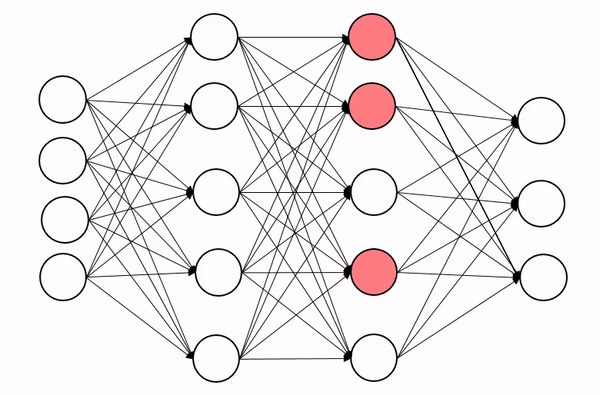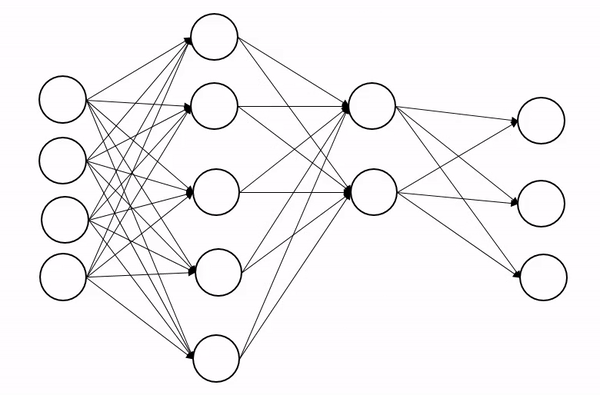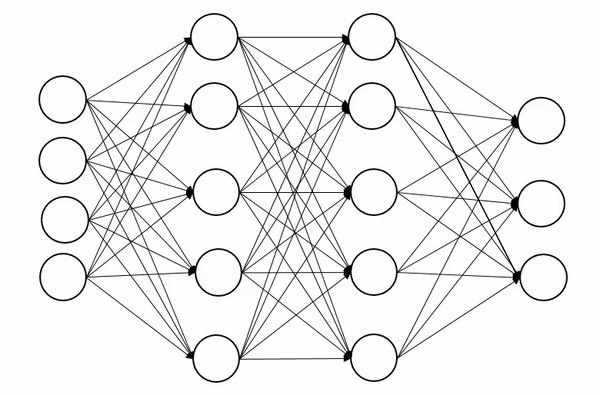
Now we can’t just zero out activations naively because this will screw up the scales across each layer. Insted we apply dropout with probability p and then rescale all activations by 1-p to keep the scales well behaved.

The resulting model from the review article thus looks like:

model = nn.Sequential(
    nn.Linear(20, 200),
    nn.ReLU(),
    nn.Linear(200, 200),
    nn.ReLU(),
    nn.Dropout(p=0.2),
    nn.Linear(200, 50),
    nn.ReLU(),
    nn.Linear(50, 50),
    nn.ReLU(),
    nn.Dropout(p=0.1),
    nn.Linear(50, 2),
)

And just like before, we can define the optimizer. In this case we’ll use a special optimizer called Adam, which combines SGD with some other techniques to speed up training. You can find the details of Adam in Chapter 16 of the fastai book, but for now, we’ll just instantiate it from PyTorch:

optimizer = torch.optim.Adam(model.parameters(), lr=lr)

fit()
print_scores()

Loss: 0.263
Accuracy: 0.890

Not bad, we’ve got a decent boost from using a deeper model and better optimizer!

Wrapping everything in a Learner#

To wrap things up, let’s show how we can feed all these building blocks into a fastai Learner that takes care of the training loop for us. First we’ll need to create a validation set for evaluation, so let’s do that using the same techniques we did for the training set:

train_ds = TensorDataset(train_x, train_y)
train_dl = DataLoader(train_ds, batch_size=bs, shuffle=True)

# Slice out all feature columns and cast to float32
valid_x = valid_df.iloc[:, :-1].values
valid_x = scaler.fit_transform(valid_x)
valid_x = torch.from_numpy(valid_x).float()
# Slice out the label column
valid_y = torch.from_numpy(valid_df.iloc[:, -1].values)
# Create dataset and dataloader for validation set
valid_ds = TensorDataset(valid_x, valid_y)
valid_dl = DataLoader(valid_ds, batch_size=bs)

Now that we have dataloaders, recall that fastai wraps them in a single DataLoaders object:

dls = DataLoaders(train_dl, valid_dl)

The final step is to define the model and optimizer:

model = nn.Sequential(
    nn.Linear(20, 200),
    nn.ReLU(),
    nn.Linear(200, 200),
    nn.ReLU(),
    nn.Dropout(p=0.2),
    nn.Linear(200, 50),
    nn.ReLU(),
    nn.Linear(50, 50),
    nn.ReLU(),
    nn.Dropout(p=0.1),
    nn.Linear(50, 2),
)

opt_func = Adam

and wrap everything in a Learner and train for 3 epochs:

learn = Learner(dls, model, loss_func, opt_func=opt_func, metrics=[accuracy])

learn.fit(3, lr)

epoch	train_loss	valid_loss	accuracy	time
0	0.251400	0.311221	0.834794	00:13
1	0.243241	0.369533	0.796215	00:13
2	0.242842	0.313126	0.863372	00:13

Well, this was quite a deep dive into traiing neural networks from scratch and ending with with all the components that go into a fastai Learner!

Next week, we’ll move away from tabular data and take a look a class of neural networks for images that are based on convolutions 👀.

Exercises#

Instead of using nn.Sequential to create our neural network, try implementing this as a subclass of nn.Module and training the resulting model.
Using the validation dataset and dataloader, try computing the validation loss and accuracy within the fit() function.
Read the Xavier initialization paper

Deep Learning for Particle Physicists

Lecture 3 - Neural network deep dive

Contents

Lecture 3 - Neural network deep dive#

Learning objectives#

References#

Setup#

Imports#

The dataset#

Preparing the data#

Logistic regression as a neural network#

Refactoring with PyTorch’s functional API#

Refactoring with PyTorch’s `nn` classes#

Refactoring with PyTorch optimizers#

Refactoring with `Dataset` classes#

Refactoring with DataLoaders#

Going deeper#

Wrapping everything in a Learner#

Exercises#

Deep Learning for Particle Physicists

Lecture 3 - Neural network deep dive

Contents

Lecture 3 - Neural network deep dive#

Learning objectives#

References#

Setup#

Imports#

The dataset#

Preparing the data#

Logistic regression as a neural network#

Refactoring with PyTorch’s functional API#

Refactoring with PyTorch’s nn classes#

Refactoring with PyTorch optimizers#

Refactoring with Dataset classes#

Refactoring with DataLoaders#

Going deeper#

Wrapping everything in a Learner#

Exercises#

Refactoring with PyTorch’s `nn` classes#

Refactoring with `Dataset` classes#