This week I mostly worked on getting my knowledge distillation code up and running, doing some pair-programming with Leandro von Werra to re-implement Google's Unsupervised Data Augmentation for Consistency Training, and reviewing a book chapter on decoding strategies for text generation.

$(\mathrm{DistilBERT})^2$

I extended my question answering analysis with transformers to implement a proof-of-concept for task-specific knowledge distillation.¹ Unlike task-agnostic distillation where the transfer of knowledge from teacher to student is done during pretraining, the task-specific approach involves using a teacher to augment the cross-entropy loss of the student during finetuning:

$${\cal L}(\mathbf{x}|T) = - \sum_i \bar{y}_i\log y_i(\mathbf{x}|T) -T^2 \sum_i \hat{y}_i(\mathbf{x}|T)\log y_i(\mathbf{x}|T)$$

Here $T$ is the temperature, $\hat{y}$ are the outputs from the model, $\bar{y}$ the ground-truth labels, and $y_i$ a softmax with temperature.

This neat idea comes from the DistilBERT paper, where the authors found that including a "second step of distillation" produced a student that performed better than simply finetuning the distilled language model:

We also studied whether we could add another step of distillation during the adaptation phase by fine-tuning DistilBERT on SQuAD using a BERT model previously fine-tuned on SQuAD as a teacher for an additional term in the loss (knowledge distillation). In this setting, there are thus two successive steps of distillation, one during the pre-training phase and one during the adaptation phase. In this case, we were able to reach interesting performances given the size of the model:79.8 F1 and 70.4 EM, i.e. within 3 points of the full model.

A comparison of the two approaches is shown in the figure below:

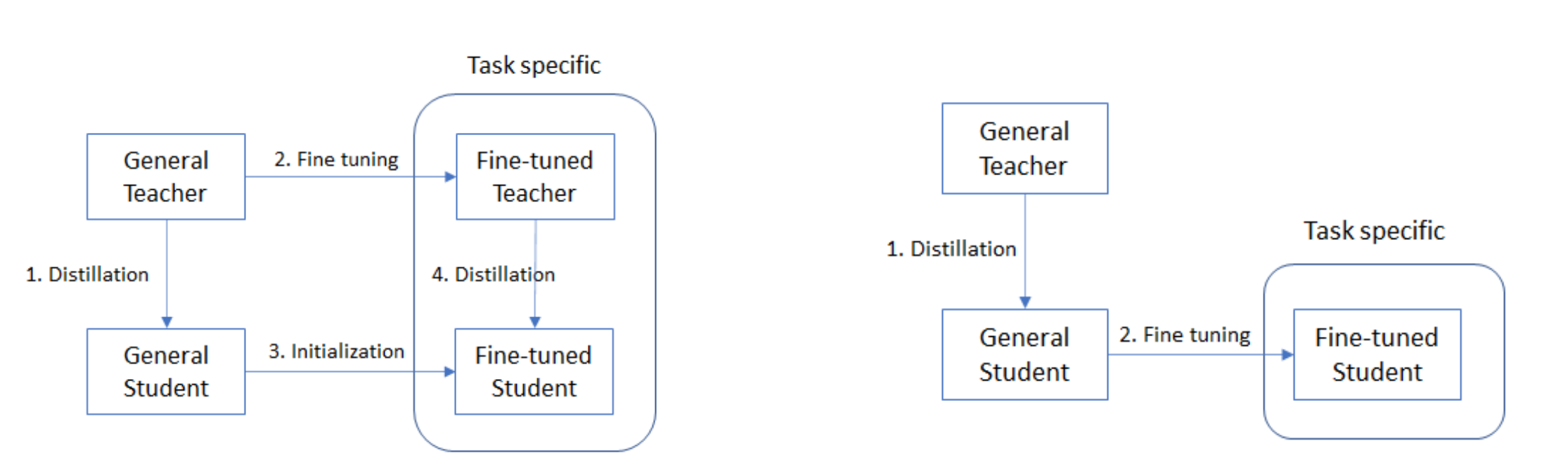
I find this idea to be quite appealing for deploying Transformers in production environments as we get the benefits of speed from using a distilled language model, yet largely preserve the performance of the teacher.

So my task this week was to reproduce the SQuAD v1.1 results from Table 2 of the DistilBERT paper. To do this I integrated Sylvain Gugger's question answering material (see last weeknotes) together with Victor Sanh's implementation of knowledge distillation.²

The main bit of work was to create a Trainer class that could:

handle two models at once, i.e. for the teacher and student
run evaluation during training to get feedback on the distillation process

The solution I ended up with involved subclassing the QuestionAnsweringTrainer I had previously adapted from Sylvain and simply overriding the compute_loss function:

class DistillationTrainer(QuestionAnsweringTrainer):
    def __init__(self, *args, teacher_model=None, **kwargs):
        super().__init__(*args, **kwargs)
        self.teacher = teacher_model
        self.teacher.eval()
        ...

    def compute_loss(self, model, inputs):
        inputs_stu = {...}
        outputs_stu = model(**inputs_stu)
        loss = outputs_stu.loss
        start_logits_stu = outputs_stu.start_logits
        end_logits_stu = outputs_stu.end_logits

        with torch.no_grad():
            outputs_tea = self.teacher(**inputs)
            start_logits_tea = outputs_tea.start_logits
            end_logits_tea = outputs_tea.end_logits

        loss_fct = nn.KLDivLoss(reduction="batchmean")
        loss_start = (
            loss_fct(
                F.log_softmax(start_logits_stu / self.args.temperature, dim=-1),
                F.softmax(start_logits_tea / self.args.temperature, dim=-1))
            * (self.args.temperature ** 2))
        loss_end = (
            loss_fct(
                F.log_softmax(end_logits_stu / self.args.temperature, dim=-1),
                F.softmax(end_logits_tea / self.args.temperature, dim=-1))
            * (self.args.temperature ** 2))
        loss_ce = (loss_start + loss_end) / 2.0
        loss = self.args.alpha_ce * loss_ce + self.args.alpha_squad * loss
        return loss

By using DistilBERT-base as the student and BERT-base fine-tuned on SQuAD v1.1 as the teacher, I was able to get within spitting distance of the published results (Exact Match/F1 = 79.1/86.9), with the differences likely due to the choice of hyperparameters:

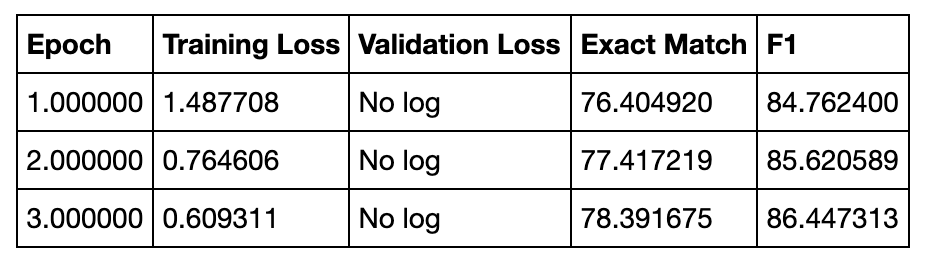
Overall, I'm pretty happy with how this turned out and am starting to appreciate the power of the "trainer paradigm", where one can abstract away tons of boilerplate (and error-prone) code for the training loop, evaluation, prediction etc and just focus on overriding the parts you need. I'm looking forward to pushing this analysis one step further with pruning and quantization - that's on the menu for next week!

Papers this week

This week I've been reading up on OpenAI's GPT papers to better understand how decoding methods for text generation work with conditional language models:

Language Models are Unsupervised Multitask Learners by Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, Ilya Sutskever (2019)
Language Models are Few-Shot Learners by Tom B. Brown et al. (2020)

TIL this week

Recovering columns hidden by the 🤗 Trainer

1. As far as I know, this term was coined in the FastFormers: Highly Efficient Transformer Models for Natural Language Understanding paper by Y. Kim and H. Awadalla in their↩

2. Thanks to Thomas Wolf for pointing me to this resource.↩